PRINCIPIOS DE LA GESTIÓN DE INVENTARIOS

Los principios que se presentaran a continuación son indispensable para no tener ningun tipo de inconveniente en la administración de inventarios, cualquier violación a estos es sin duda un error grave que se puede cometer. Estos principios son:

1. Toda entrada y salida del inventario debe estar debidamente documentada.

2. Todo ítem (producto, elemento guardado en un inventario) debe estar debidamente codificado.

3. En cuanto sea posible, todos los ítems deben estar guardados en el mismo lugar.

4. Nunca jamás recibir comisiones de un proveedor.

5. En cuanto sea posible, el lugar físico donde se realiza la recepción de la materia prima debe ser diferente al lugar donde se hace la salida de materiales.

6. Los ítems de mayor peso o masa deben estar ordenados desde menor a mayor peso.

7. Ningún miembro del equipo del almacén se puede ir hasta que no haya un conteo de los ítems que tuvieron movimiento en ese día.

8. Se debe contar por tres auditores diferentes los mismos ítems y se consignan los dos iguales.

9. El punto más lejos de un inventario debe haber un extintor.

10. Los reportes de inventarios deben estar como máximo 3 días después del cierre del ciclo contable.

SISTEMA DE INVENTARIOS ABC

Se puede afirmar que uno de los primeros pasos para la administración y análisis de un sistema de inventarios es realizar un análisis ABC. Este sistema permite determinar que artículos representan la mayor parte de la inversión y si se justifica mantener invertidos estos recursos.

El sistema ABC utiliza el principio económico planteado por VILFREDO PARETO, quien estudió la distribución de la riqueza en el siglo XIX: Gran parte de la riqueza pertenece a un pequeño segmento de la población.

Ford Dickie (1951) aplica este principio a la administración de inventarios y lo llamó análisis ABC. Dado que mantener un nivel de inventario implica un capital inactivo es natural que se ejerza un control sobre aquellos artículos que representen una mayor inversión en capital, al contrario aquellos artículos que contribuyen muy poco en la inversión en capital merecen poca atención.

El Sistema ABC permite establecer y determinar en una forma sencilla cuales artículos son de mayor valor y cuales de menor valor de manera que se pueda tomar decisiones eficientes lo cual permite optimizar la administración de recursos asignados a los inventarios.

El sistema ABC clasifica los artículos del inventario en tres grupos:

Grupo A: Se incluyen los artículos más importantes para efectos de control.

Aquellos que contribuyen al 80% del valor monetario acumulado y generalmente constituyen alrededor del 20% de los artículos. Como se puede apreciar representan pequeñas cantidades de artículos costosos los cuales deben estar sujetos a un estrecho control, se utilizan procedimientos complejos de pronóstico y debe tenerse cuidado al estimar los diversos parámetros de costo para establecer las políticas de operación.

Grupo B: Corresponde a aquellos artículos de importancia secundaria, corresponden a valores monetarios porcentuales entre el 80% y el 95%, y comprende alrededor del 25% de todos los artículos. A estos artículos se les aplica un control moderado, los artículos se pueden revisar de forma periódica, se solicitan por grupos y no de forma individual y se utilizan métodos de pronóstico menos complicados.

Grupo C: Son artículos de importancia reducida, corresponden entonces al 5% del valor monetario porcentual y comprenden mas o menos el 55% de los artículos. A estos artículos se les ejerce un grado mínimo de control, se deben realizar pedidos de gran tamaño con el fin de minimizar la frecuencia de pedidos Esta clasificación es arbitraria pudiendo existir un número diferente de grupos. Si se desea un mayor refinamiento, también el % exacto de artículos de cada clase varía de un inventario al siguiente. Esta relación empírica formulada por Wilfredo Pareto, ha demostrado ser una herramienta muy útil y sencilla de aplicar a la gestión empresaria. Permite concentrar la atención y los esfuerzos sobre las causas más importantes de lo que se quiere controlar y mejorar.

El procedimiento a seguir para el sistema e inventarios ABC es el siguiente:

a) Determinar la participación monetaria de cada artículo en el valor total del inventario. (Multiplicar el costo unitario de cada artículo por el número total de unidades demandadas).

b) Calcular porcentaje acumulado de artículos basado en el número total de artículos.

c) Calcular porcentaje acumulado de uso del dinero basado en el uso total.

d) Tabular los artículos del inventario en orden descendente según el total de dinero invertido en cada ítem del inventario.

e) Graficar la curva ABC del porcentaje acumulado del uso del dinero en función del porcentaje acumulado de artículos.

Ejemplo: Clasificar por el sistema ABC los Productos que se presentan en la tabla 1.

Tabla 1: Datos del ejemplo ABC

Solución:

1. Calcular la participación monetaria de cada artículo en el valor total del inventario. Ver tabla 2; para hallar el uso anual de dinero se multiplica precio unitario por la cantidad utilizada.

2. Para hallar el porcentaje de uso anual de dinero se divide la información del uso anual del dinero entre el total de esta columna.

Tabla 2: Solución ABC.

3. se tabula la información en orden descendente según el porcentaje del uso anual del dinero.

A continuación se presenta un ejemplo desarrollado por el ing Tomas A. r. Fucci que permitirá visualizar cómo se determinan las tres zonas (A-B-C) en un inventario constituido por 20 artículos:

Solución

Se debe determinar la participación monetaria de cada artículo en el valor total del inventario. Para ello se debe construir una tabla (ver tabla 23) de acuerdo a lo siguiente:

Columna nº 1: Corresponde al nº de artículo.

Columna nº 2: Los porcentajes de participación de cada artículo en la cantidad total de artículos. Para nuestro ejemplo, como tenemos un inventario constituido por 20 artículos, cada artículo representa el 5% dentro del total (100%/ 20 art.= 5%)

Columna nº 3: Representa la valorización de cada artículo. Para obtenerla, multiplicamos su precio unitario por su consumo. Al pie de la columna obtenemos el valor de nuestro inventario de los 20 artículos.

Columna nº 4: Nos muestra el % que representa cada una de las valorizaciones en el valor total del inventario.

2. Ahora se deben reordenar las columnas 1 y 4, tomando las participaciones de cada artículo en sentido decreciente, lo que dará origen a la tabla 4.

Tabla 4. Determinación de la participación monetaria de cada artículo en el valor total de inventario.

3. Trazado de la gráfica y determinación de zonas ABC.

A partir de los datos de la tabla 23 y la gráfica se puede observar que unos pocos artículos son los de mayor valorización. Si solo se controlaran estrictamente los tres primeros, se estaría controlando aproximadamente el 60% del valor del inventario.

Asignamos la zona A para estos artículos. Controlando también los art. 3, 6 y 11, se estaría controlando, en forma aproximada, el 82% del valor del inventario.

(Zona B)

Se ve claramente en la gráfica que el 15% del inventario justifica el 60% del valor, mientras que el 30% del mismo justifica el 82% de dicho valor; a su vez, el 70% del inventario justifica el 18% del valor. Si se tiene en cuenta los costos de mantenimiento y de control de estos últimos, se llega a la conclusión que no es necesario controlarlos estrictamente, ya que son de poca valorización, y que debe mantenerse el mínimo stock posible de los mismos.

La asignación de las zonas A, B y C en la gráfica que estamos analizando se realizó en función del alto % de valorización de los tres primeros artículos (25,47%, 18.55% y 16.08%, respectivamente), sin embargo, las zonas pueden asignarse de forma diferente, por ejemplo, incluyendo en la zona A los seis primeros artículos, que representan alrededor del 80% del valor del inventario, en la zona B los siguientes tres artículos, y los restantes en la zona C. De esta forma, controlando el 30% del inventario (zona A) se estaría controlando aproximadamente el 80% del valor del mismo.

Observando las zonas A y B de la gráfica que se da a continuación, se puede ver que el 45% del inventario justifica alrededor del 90% de su valor y que el 55% del inventario justifica, aproximadamente, el 10% del mismo valor.

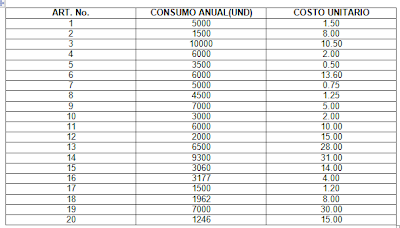
DESCARGAR ARCHIVO DE EXCEL

TEORIA DE DECISIONES

La teoría de decisiones se usa como proceso racional para seleccionar la mejor de varias alternativas. La teoria de decisiones agrupa la toma de decisiones en las siguientes 3 categorías:

1. Toma de decisiones bajo certidumbre

2. Toma de decisiones bajos riesgo

3. Toma de decisiones bajo incertidumbre

1. Toma de decisiones bajo certidumbre

Son aquellas en donde todas las variables se encuentran bien definidas.

2. Toma de decisiones bajos riesgo

En condiciones de riesgo, las ventajas asociadas a cada alternativa de decision se describen con distribuciones de probabilidad. Se utiliza el criterio de valor esperado y la alternativa que maximiza el valor esperado es la que se escoge.

3. Toma de decisiones bajo incertidumbre

La toma de decisiones bajo incertidumbre, al igual que bajo riesgo, implica acciones alternativas cuyas retribuciones dependen de los estados de la naturaleza (Aleatorios).

Para la solución de este tipo de decisiones se utilizan los siguientes criterios de análisis:

1. Laplace o principio de la razón insuficiente.

2. Minimax o elección de mejor entre las peores posibles

3. Savage o criterio de pasadumbre

4. Hurwicz

VIDEO SOBRE TEORIA DE DECISIONES

TEORIA DE JUEGOS

La teoría de juegos maneja situaciones de decisión en la que intervienen 2 jugadores inteligentes que tienen objetivos contrarios. Un ejemplo de esto es las estrategias belicas utilizadas en la guerra, las campañas publicitarias, etc.

En el juego intervienen 2 oponentes llamados "jugadores", y cada uno tiene un numero finito o infinito de alternativas o "Estrategias".

La teoría de juegos fue desarrollada antes de la guerra fría y se formalizo con los trabajos de John Von Neumann y Oskar Morgenstern.

Actualmente tiene muchos campos de aplicación como lo es: Biología, Sociología, Filosofía, Inteligencia Artificial y cibernetica.

Un juego se puede representar en una matriz donde cada elemento de esta corresponde a la recompensa que obtendrá el jugador Fila al utilizar la estrategia i si el jugador columna utiliza la estrategia j.

Lo anterior se muestra a continuación:

También en teoría de juegos existe el criterio de Minimax y Maximin.

Minimax:

El jugador fila, elige que su pago mínimo posible sea el mayor.

Maximin:

Criterio Minimax: el jugador B elige que el pago máximo a A sea el menor posible.

En particular estudiaremos los juegos de suma cero que se explican a continuación:

JUEGOS DE SUMA CERO

En los juegos de suma cero el beneficio total para todos los jugadores del juego, en cada combinación de estrategias, siempre suma cero (en otras palabras, un jugador se beneficia solamente a expensas de otros). El go, el ajedrez, el póker y el juego del oso son ejemplos de juegos de suma cero, porque se gana exactamente la cantidad que pierde el oponente. Como curiosidad, el fútbol dejó hace unos años de ser de suma cero, pues las victorias reportaban 2 puntos y el empate 1 (considérese que ambos equipos parten inicialmente con 1 punto), mientras que en la actualidad las victorias reportan 3 puntos y el empate 1.

ESTRATEGIA DOMINANTE

Se dice que un jugador posee una estrategia dominante si una estrategia particular es preferida a cualquier otra estrategia a disposición de el. Es posible que cada uno de los dos jugadores tenga estrategia dominante.

ESTRATEGIA MIXTA

Es una combinación de dos estrategias escogidas a azar, una cada vez, según determinadas probabilidades, en contraste con una estrategia pura que no contiene tales elementos de azar.

PUNTO SILLA

También conocido como punto de ensilladura, es un punto donde la recompensa que obtiene el jugador Renglón es igual a la del jugador columna.

Ejemplos:

Supongamos que 2 jugadores juegan en cierto juego. Del juego se sabe que tienen la siguiente matriz premio:

Ahora se debe definir con que frecuencia el jugador Renglón y el jugador Columna usan sus estrategias. Para resolver este problema se puede usar el método grafico y el método algebraico. Aunque el método algebraico cuando hay mas de 2 alternativas se vuelve tedioso por lo que se utilizara el método simplex.

Método Algebraico:

Ahora se introducira el concepto de valor esperado de una estrategia cuando los jugadores utilizan una estrategia determinada.

La finalidad es buscar aquella estrategia que me de el mayor valor esperado. Gráficamente seria la intersección de las curvas de valor esperado de E1 y E2.

Ahora se hace igualmente para la estrategia 2 del jugador renglón.

Graficando lo anterior obtenemos:

Por lo que se obtiene que el valor Esperado que maximiza el juego para el jugador renglon es: 0.5 con probabilidades de utilizar cada estrategia de 0.5

CADENAS DE MARKOV

De manera formal las cadenas de Markov se definen como:

Otra explicación es:

Para poder definir las cadenas de Markov primero debe definirse lo que es un Proceso de Markov:

PROCESO DE MARKOV

Un proceso de Markov es aquel en que la probabilidad de ocurrencia de un estado futuro depende del estado inmediatamente anterior.

Las cadenas de Markov representan o modelan el comportamiento de estos sistemas, de forma que se puede conocer la probabilidad de cambiar de un estado a otro.

Principios de las cadenas de Markov

1. La matriz de transición debe ser cuadrada.

2. Las probabilidades de los estados entre 0 y 1.

3. Las suma de las probabilidades de los estados es igual a 1.

Las cadenas de Markov, como se definió anteriormente se representan en matrices, y de acuerdo al tipo de arreglo que tenga la matriz estas se pueden clasificar en:

1. Matriz regular

Es una un arreglo donde los elementos de una matriz son diferentes de 0 y 1.

2. Matriz Absorbentes

Es un arreglo donde un estado de la cadena de Markov es igual a 1.

3. Matriz Ergodica

Si los estados en una cadena son recurrentes, aperiodicos y se comunican entre si, se dice que la cadena es ergódica.

Ejemplos de Matriz Ergodica

Una características de las cadenas es que se pueden representar por medio de un diagrama de grafos.

El siguiente ejemplo ilustra lo anterior:

Ejemplo 2:

1. Una computadora se inspecciona cada hora. Se encuentra que está trabajando o descompuesta. Si está trabajando la probabilidad de que siga trabajando la siguiente hora es 0.9 Si está descompuesta, se toman las medidas para repararla lo que puede llevar más de una hora. Siempre que la computadora esté descompuesta, Independientemente de cuanto tiempo haya pasado, la probabilidad de que siga descompuesta la siguiente hora es 0.35.

A. Modele el sistema como una cadena de Markov.

Solución:

Debemos definir los estados

Eo = La maquina está trabajando

E1 = La maquina está descompuesta

	Eo	E1
Eo	0.9	0.1
E1	0.65	0.35

B. Hoy está trabajando, ¿Cuál es la probabilidad de que en 4 hrs sigatrabajando

Solución:

Buscamos T⁴ = P(4)

T⁴ =

	Eo	E1
Eo	0.85	0.15
E1	0.84	0.16

Ejemplo 3:

2. Un fabricante de grabadoras está tan seguro de su calidad que está ofreciendo garantía de reposición total si el aparato falla en dos años. Basándose en datos compilados la compañía ha notado que solo el 1 % de las grabadoras falla durante el primer año y 5 % durante el segundo. La garantía no cubre grabadoras ya reemplazadas.

A. Modele el sistema como una cadena de Markov.

Solución:

Debemos definir los estados

Eo = Está funcionando en su primer año.

E1 = Está funcionando en su segundo año.

E2 = Se reemplaza por garantía.

E3 = Finaliza la garantía.

	Eo	E1	E2	E3
Eo	0	0.99	0.01	0
E1	0	0	0.05	0.95
E2	0	0	1	0
E3	0	0	0	1

Ejemplo con videos:

EOQ probabilistico

MODELO DE INVENTARIO EOQ PROBABILÍSTICO

En muchas situaciones es de utilidad utilizar distribuciones de probabilidad para describir el comportamiento de la demanda de un modelo.

La naturaleza probabilística de la demanda cuando se desea pronosticar la demanda de un bien, permite determinar el nivel de servicio que desea optar una organización. Se entiende por nivel de servicio el número de veces que un cliente decidió comprar nuestro producto y lo ha encontrado disponible, este se expresa en porcentaje. Matemáticamente esto quiere decir:

El nivel de servicio se puede medir en términos del número de unidades y en términos del valor de las unidades. En ambos casos el nivel de servicio es diferente. La utilización de uno con respecto a otro depende de cómo la organización desea medir este indicador.

Se supondrá que la demanda se encuentra distribuida normalmente, por lo tanto también se establece una cantidad promedio que denotaremos por µ y una desviación estándar ϑ (Sigma), de manera que si se le resta y se le suma a la cantidad promedio 3 veces ϑ se obtendrá el 99.74% del área bajo la curva de la distribución. La siguiente imagen muestra lo anterior:

Aplicando este principio al modelo EOQ, el valor de µ es el valor medio o valor esperado de la demanda de un bien, y ϑ es la desviación que tiene dicha demanda siendo los resultados mas probables de ocurrir las que se encuentran mas cerca de µ.

Ejemplo:

Una empresa tiene una demanda promedio mensual de 500 bombillas con una desviación estándar de 50.

Del anterior ejemplo se concluye que es mucho más probable que la demanda en dicho este entre 350 y 650 (Sumándole y restándole 3 veces la desviación estándar).

Para poder aplicar este modelo se debe definir con antelación el nivel de significancia o el numero de de ordenes que no podrán ser atendidas. Para el lector es difícil comprender esto ¿Cómo así que no todos lo clientes podrán adquirir nuestro producto? Bueno para responder esto se tiene que recordar que mantener una gran cantidad de inventario para responder la demanda de un bien y así satisfacer todos los clientes seria algo muy costoso, por lo que las organizaciones usan el concepto de “Porcentaje de Nivel de Servicio”, o en otras palabras fijan de una cantidad de 100 clientes a cuantos están dispuestos a satisfacer.

Gráficamente se expresa así:

Según el grafico de cada 100 pedidos 5% de ellos no se podrán cumplir según la política de inventario. (0.05 al expresarse en porcentaje resulta 5%).

A todo el inventario adicional que se tiene des pues de la media se le denomina Stock o inventario de Seguridad, que se define como el inventario que se tiene adicional para poder responder a cualquier cambio abrupto en la demanda.

Se define como:

Donde z, es el valor del nivel de significancia en la tabla de distribución normal estandarizada.

En el siguiente link se encuentra la tabla de distribución normal estandarizada:

http://www.uam.es/personal_pdi/ciencias/barcelo/modelos-matematicos-biologia/tabla_normal2.jpg

Ahora el inventario total que debe tener una organización se define como el inventario promedio más el inventario de seguridad. Matemáticamente:

Nota:

Debe tenerse presente que en situaciones el tiempo de espera difiere del tiempo que se tienen los datos de la demanda.

Por ejemplo:

Suponga que se tiene una demanda semanal µ=200 unidades, con una desviación estándar ϑ, además se sabe que el tiempo de suministro es de 2 semanas. ¿Se desea saber cuanto inventario almacenar para poder responder a la demanda para mantener un nivel de servicio del 90%?

Solución:

Se observa que el tiempo de suministro difiere del tiempo en que se encuentra la demanda y su desviación estándar. El procedimiento a seguir para calcular el inventario que se debe almacenar es la siguiente:

Donde L, es el tiempo en que se encuentra el tiempo de suministro

Para un nivel de servicio del 90% buscando en la tabla de distribución normal obtenemos que el valor estandarizado es: Z = 1.28 para un valor en la tabla de 0.8997

Se redondea 90.5 a 91, y se obtiene:

Para un tiempo de suministro de 2 semanas, se debe almacenar un inventario total de 491 unidades para mantener un nivel de servicio del 90%.

Lo anterior se puede formular así: Para obtener la desviación estándar en un tiempo diferente al que se tiene originalmente se procede:

Donde ϑl, es la desviación estándar en el tiempo que se desea calcular

ϑt, es la desviación estándar en el periodo de tiempo que se tiene.

L, es el numero de periodos.

Textos de referencia:

Taha Handy, Investigacion de Operaciones

Krajewsky Lee, Administracion de Operaciones